edx 课程《Introduction to Probability - The Science of Uncertainty》Unit3 笔记
Unit3 Counting
1. Discrete uniform law
假设样本空间 $\Omega$ 由 $n$ 个等可能的元素组成
假设 $A$ 由 $k$ 个元素组成
那么,我们有 $P(A) = \frac{number \ of \ elements \ of \ A}{number \ of \ elements \ of \ \Omega} = \frac{k}{n}$
2. Basic counting principle
Example1
假设你一大早起来了,准备一天的着装打扮,你发现,你有 4 件T恤, 3 条领带, 2 件夹克,那么你今天有几种着装方式呢?
这个问题的答案其实很简单。我们把着装看成一个序列化的过程,一共有3个阶段,第一阶段选择T恤,第二阶段选择领带,第三阶段选择夹克。那么,一共有 $4 \times 3 \times 2 = 24$ 种选择。
Example2
车牌号由 2 个字母后面接 3 个数字组成,那么一共有多少种车牌号呢?
将这个问题看成一个序列化的问题,在第一阶段,我们选择字母,第一个字母,我们有 26 种选择。第二个字母,我们又有 26 种选择。第二阶段,我们选择数字,第一个数字, 10 种选择,第二个数字,也是 10 种选择,第三个数组还是 10 种选择。所以一共有 $26 \times 26 \times 10 \times 10 \times 10$
现在,我们给这个问题加上一些限制条件。
- 如果数字和字母不能重复出现,那么一共有多少种车牌号呢?
同样看成一个序列化的问题,第一阶段选择字母,第一个字母,我们有 26 种选择,因为字母不能重复出现,所以第二个字母,我们只有 25 种选择。第二阶段,我们选择数字, 第一个数字有 10 种选择,第二数字就有 9 种, 第三个数字只有 8 种了。所以一共有 $26 \times 25 \times 10 \times 9 \times 8$
2.1 permutation(排列)
给 $n$ 个元素进行排序就是排列。
Number of ways of ordering $n$ elements: $n \cdot (n-1) \cdot (n-2) … \cdot 1 = n !$
集合的大小为 $n$,那么这个集合的子集数目应该是:
Number of subsets of ${ 1, …, n }$ : $2 \cdot 2 \cdot 2 \cdot … \cdot 2 = 2^n$
2.2 combination(组合)
给定 $n$ 个元素,我们想要从这 $n$ 个元素中选出 $k$ 个,组成一个新的子集,那么一共有几种选法?
Defintion $(_k^n )$: number of k-elements subsets of a given n-elements set
我们有两种方式从 $n$ 个元素中去构建一个有序的,长度为 $k$ 的,元素不重复的序列:
- 1.每次选择一个元素,一共选择 $k$ 次。
这样选择之后,我们一共有 $n\cdot (n-1) \cdot (n-2) … \cdot (n-k+1) =\frac{n!}{(n-k)!}$ 种选择。
- 2.选择 $k$ 个元素,然后对他们进行排列。
这样的方式得到的结果应该是 $(_k^n ) \cdot k!$
两种方式得到的结果应该相等,所以 $(_k^n ) = \frac{n!}{k!(n-k)!}$
值得一提的是 $0! = 1$
另外,还有一个常用的式子是:
$$\sum_{k=0}^n (_k^n ) = (_0^n ) + (_1^n ) + (_2^n ) + … + (_n^n ) = # \ any \ subsets = 2^n$$
2.3 Binomial probabilities
现在有一个硬币,考虑投掷 $n$ 次,每次投掷都是独立的,且投掷到正面的概率为 $P(H) = p$
- 投掷情况为 $P(HTTHHH)$ 的概率为多少?
$$P(HTTHHH) = p(1-p)(1-p)ppp = p^4 (1-p)^2$$
- 投掷情况是一个特定序列的概率是多少?
$$P(particular \ sequence) = p^{head} (1-p)^{tail}$$
- 投掷情况是一个已知的特定序列,且该序列中有 $k$ 个 head,那么概率是多少?
$$P(particular \ k - head \ sequence) = p^k (1-p)^{n-k}$$
- 现在只知道投掷的结果是 $k$ 个heads,那么概率是多少?
$$P(k \ heads) = p^k (1-p)^{n-k} (k-head \ sequences)$$
跟上面的不同,这次我们仅仅知道投掷的结果中有 $k$ 个heads, 但是我们不知道这 $k$ 个heads的序列。所以,该结果可以看作是先求 $k$ 个heads出现的概率,再求它们可能的排列方式。
所以最后得出的结果应该是 $P(k \ heads) = (_k^n) p^k (1-p)^{n-k}$
2.4 一个例子
已知,在10次投掷中,有3次 heads,且投掷出现 head 的概率是 $P(H) = p$ 那么在这10次投掷中,前两次投掷是 heads 的概率是多少?
解答:
我们先定义两个事件
事件 $A$ :前两次投掷是 heads
事件 $B$ :在10次投掷中,有3次 heads
那么我们所求的结果应该是 $P(A|B) = \frac{P(A \cap B)}{P(B)}$
其中 $P(B) = (_3^10) p^3 (1-p)^7$, $P(A \cap B) = p^2 (_1^8) p (1-p)^7$
所以 $P(A|B) = \frac{p^2 (_1^8) p (1-p)^7}{(_3^10) p^3 (1-p)^7} = \frac{(_1^8)}{(_3^10)} = \frac{1}{15}$
2.5 Partitions and multinomial coefficient (划分和多项式系数)
给定 $n$ 个商品和 $r$ 个人,现在需要给第 $i$ 号人物 $n_i$ 个商品。
- $n_1, …, n_r$ 都是非负整数
- $n_1 + … + n_r = n$
问一共有几种分法?
假设,我们一共有 $C$ 种分法。
现在让我们换一个思考方式。跟一开始的 combination 的推理过程一样,我们假设有 $n$ 个商品,我们需要把它们排好,一共有几种排法?
- 1.每次选择一个元素,一共选择 $n$ 次。
用第一种方法,我们得到的结果应该是 $n!$
- 2.我们先把 $n$ 个商品随机的分配给 $r$ 个人。然后,我们要求第一个人把他得到的 $n_1$ 个商品进行排列,然后作为排列好的前 $n_1$个,第二个人把他得到的 $n_2$ 个商品进行排列,放在前 $n_1$ 的后面,作为接下来排列好的 $n_2$ 个商品,然后重复,一直到最后。
第二种方法,分为了两步:
第一步就是Partitions(划分),我们已经假设一共有 $C$ 种分法了。
第二步就是,针对每个部分,进行排列,一共有 $n_1 ! n_2 ! … n_r !$
所以,两步结合得到 $C n_1 ! n_2 ! … n_r !$
最后,第一种方式和第二种方式得到结果应该相等。所以
$$C n_1 ! n_2 ! … n_r ! = n! \longrightarrow C = \frac{n!}{n_1 ! n_2 ! … n_r !}$$
多项式系数(划分数目的多少) $= \frac{n!}{n_1 ! n_2 ! … n_r !}$
2.6 多项式系数的例子
问题:现在有一副牌(52张),随机地、平均地分配给4个玩家,求每个玩家都得到一张 Ace 的概率。
先计算总共的分法:$\frac{52!}{13! 13! 13! 13!}$
我们先给每个人分配一个 Ace,一共有 $4 \times 3 \times 2 \times 1$ 种分配方法,接着剩下的48张牌再平均分配,一共有$\frac{48!}{12! 12! 12! 12!}$ 种,所以两个阶段合起来就是 $4 \cdot 3 \cdot 2 \cdot \frac{48!}{12! 12! 12! 12!}$ 种。
最后结果是: $\frac{4 \cdot 3 \cdot 2 \cdot \frac{48!}{12! 12! 12! 12!}}{\frac{52!}{13! 13! 13! 13!}}$
还有另外一种更加 smart 的思考方法… 这里仅仅给出结果 $\frac{39}{51} \cdot \frac{26}{50} \cdot \frac{13}{49}$
3. 习题
- The birthday problem. Consider $n$ people who are attending a party. We assume that every person has an equal probability of being born on any day during the year, independently of everyone else, and ignore the additional complication presented by leap years (i.e., nobody is born on February 29). What is the probability that each person has a distinct birthday?
解答:
对于这 $n$ 个人,他们的样本空间 $\Omega = 365^n$,因为每个人的生日都有 365 种情况。
对于第一个人来说,他的生日选择有 $365$ 个, 第二个人只有 $364$ 个,依此类推。所以 $n$ 个人生日不相同的概率为
$$P = \frac{365!}{(365-n)! 365^n}$$
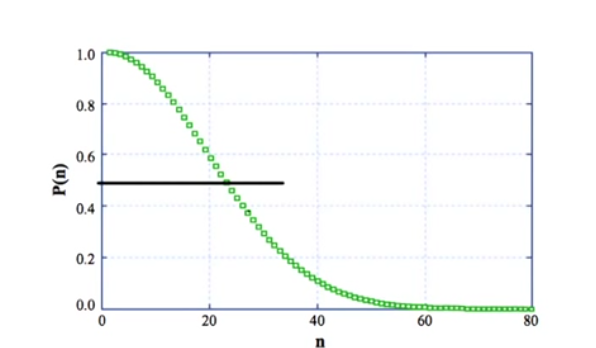
把结果用图形表示,可以看到,差不多23个人的时候,就有将近 50% 的概率碰到同一天出生的人了。
- Rooks on a chessboard. Eight rooks are placed in distinct squares of an $8×8$ chessboard, with all possible placements being equally likely. Find the probability that all the rooks are safe from one another, i.e., that there is no row or column with more than one rook.
解答:
本质上就是一个算数问题,第一个人可以有 $64$ 种摆放的位置;第二个人有 $64-15 = 49$ 种;第三个人有 $64 - 15 - 13 = 36$ 种;第四个人有 $64 - 15 - 13 - 11 = 25$ 种;第五个人有 $64 - 15 - 13 - 11 - 9 = 16$ 种;第六个人有$64 - 15 - 13 - 11 - 9 - 7 = 9$ 种;第七个人有$64 - 15 - 13 - 11 - 9 - 7 - 5 = 4$ 种;第八个人有$64 - 15 - 13 - 11 - 9 - 7 - 5 - 3 = 1$ 种;
所以,概率是 $P = \frac{64 \times 49 \times 36 \times 25 \times 16 \times 9 \times 4 \times 1}{64^8}$
- Hypergeometric probabilities. An urn contains $n$ balls, out of which exactly $m$ are red. We select $k$ of the balls at random, without replacement (i.e., selected balls are not put back into the urn before the next selection). What is the probability that $i$ of the selected balls are red?
解答:
有 $n$ 个球,其中有 $m$ 个是红色的,随机无放回地取走 $k$ 个球, 其中 $i$ 个球是红色的概率为?
看成组合问题就好了,一共有 $(^n_k)$ 种情况,有 $i$ 个红球的情况是 $(^m_i)$, 有 $k-i$ 个别的颜色的球的情况 $(^{n-m}_{k-i})$
所以总共有:
$$P = \frac{C_m^i C_{n-m}^{k-i}}{C_n^k}$$
- Multinomial probabilities. An urn contains balls of $r$ different colors. We draw $n$ balls, with different draws being independent. For any given draw, there is a probability $p_i, i=1,…,r,$ of getting a ball of color $i$. Here, the $p_i$’s are nonnegative numbers that sum to 1.
(For such independence to be possible, you may think of an urn that has infinitely many balls, so that removing one does not change the probabilities $p_i$, or you can think about drawing “with replacement”: the chosen ball is put back into the urn before the next draw.)
Let $n_1,…,n_r$ be nonnegative integers that sum to $n$. What is the probability that we obtain exactly $n_i$ balls of color $i$, for each $i=1,…,r$?
解答:
需要使用到多项式系数。
$$P(get \ type \ (n_1, n_2, …, n_r)) = \frac{n!}{n_1 ! n_2 ! … n_r !} p_1^{n_1} p_2^{n_2} … p_r^{n_r}$$